С использованием коммерческого пакета Comsol Multiphysics 3.5а получены зависимости относительного коэффициента сопротивления от числа Рейнольдса при ламинарном течении в изогнутом канале со вставкой. Диапазон радиуса кривизны от R=1D до R=4D. Проведенный комплекс численных исследований показало, что закрученный поток, попадая в изогнутую часть, образует два сложных вихря с различными размерами: наибольший располагается на внутренней части изогнутого канала. Затем эти вихри сносятся к внешней части изогнутого канала за счет сил инерции, возникающих в изогнутой трубе. Далее, по мере увеличения расстояния от входа в изогнутую часть, вихри деформируются и затухают.
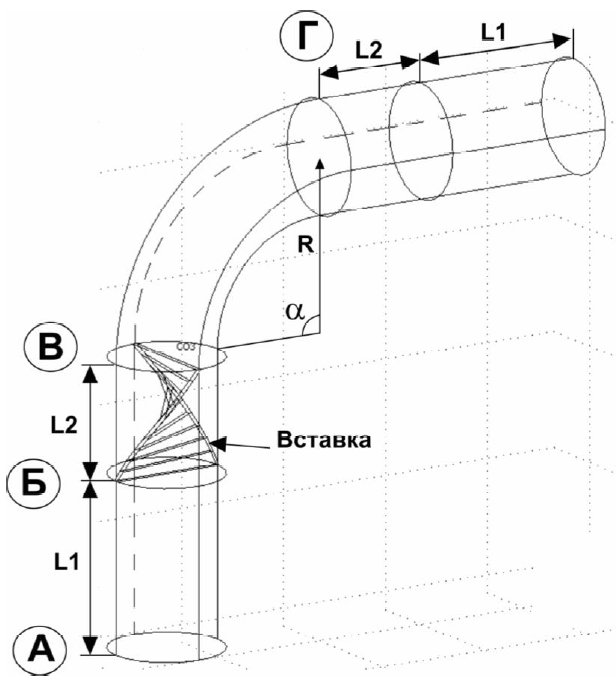
Рис. 1. Геометрия канала
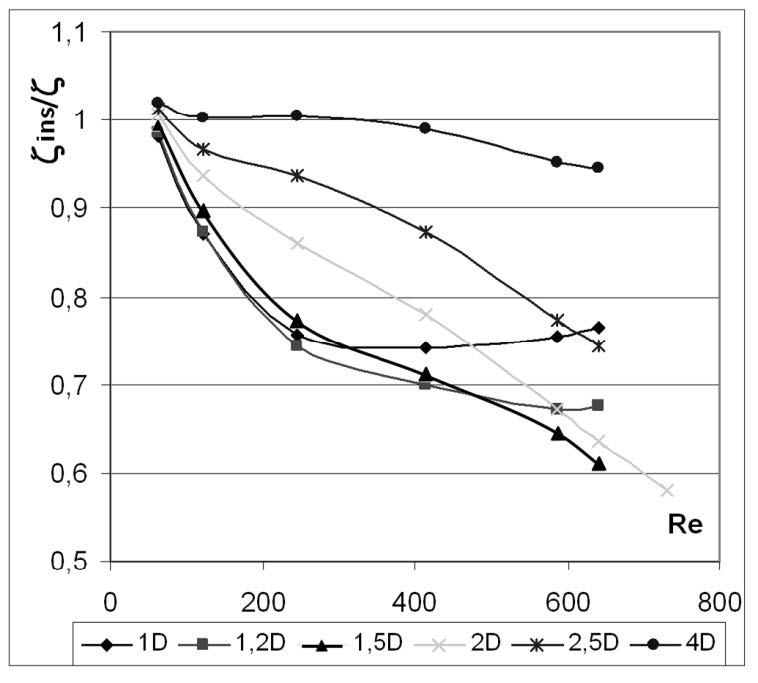
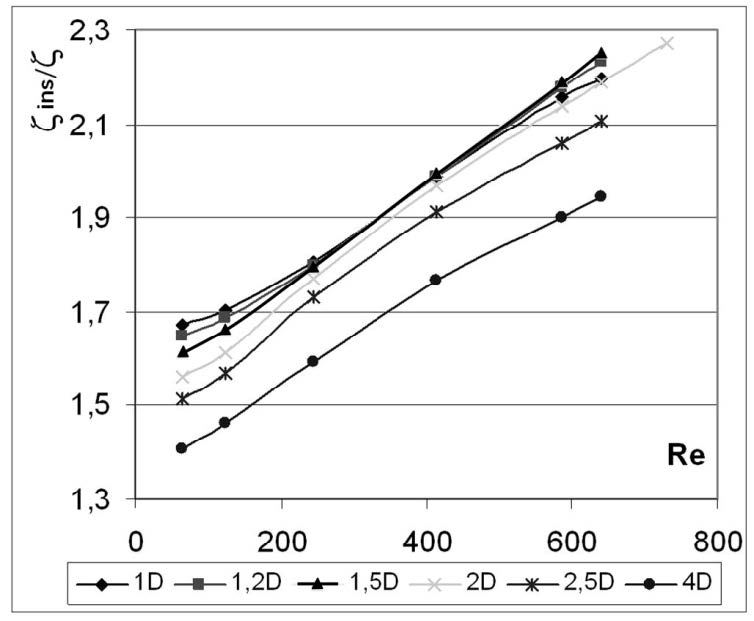
Рис. 2. Зависимость относительного местного сопротивления от числа Рейнольдса (Re) для различных вариантов радиуса кривизны отвода (R=1D…4D);
а) участок между сечениями (В) и (Г); б) участок между сечениями (А) и (Г)
Разработано аналитическое решение задачи стационарного теплопереноса при течении ньютоновской вязкой жидкости между двумя наклонными плоскостями (конфузор). Решение получено с помощью метода Фурье. По результатам температурных исследований и полей скоростей, выражения для мощности и средней температуры на выходе получают в виде серии. Проблема течения жидкости в плоском щелевом канале была решена аналогично. На основании полученных формул тепловых и гидродинамических полей для потока воды в канале конвергентного были вычислены. было произведено сравнение тепловой эффективности конвергентных и плоских каналов временных интервалов.
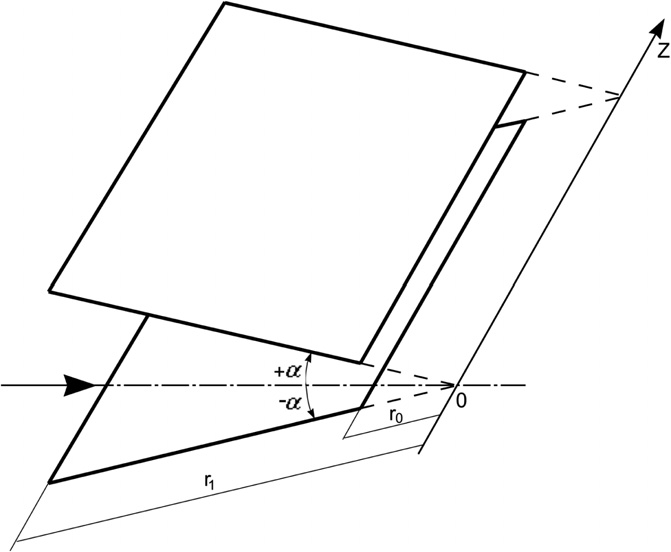
Рис. 3. Геометрия канала
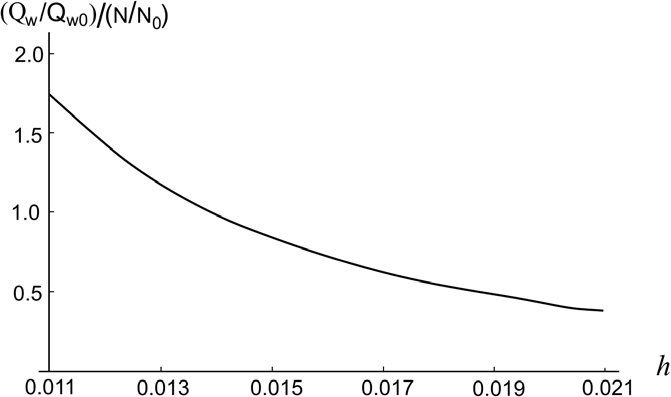
Рис. 4. Теплогидродинамическая эффективность конвергентного канала
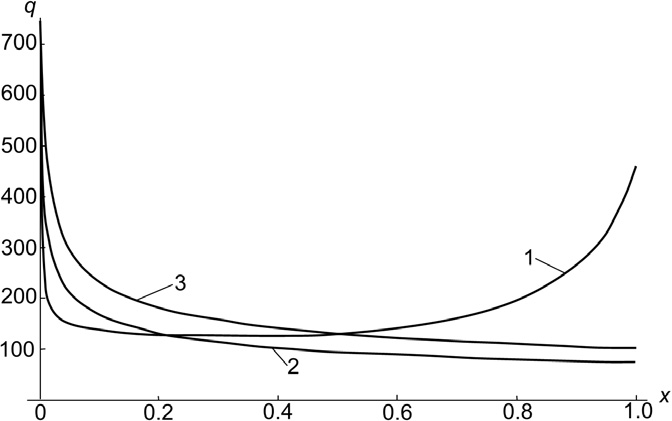
Рис. 5. Распределение плотности теплового потока вдоль стенок конвергентного и плоского каналов: 1 – конвергентный канал, 2 – плоский канала с h=0.018 м; 2 – плоский канал с h=0.013 м
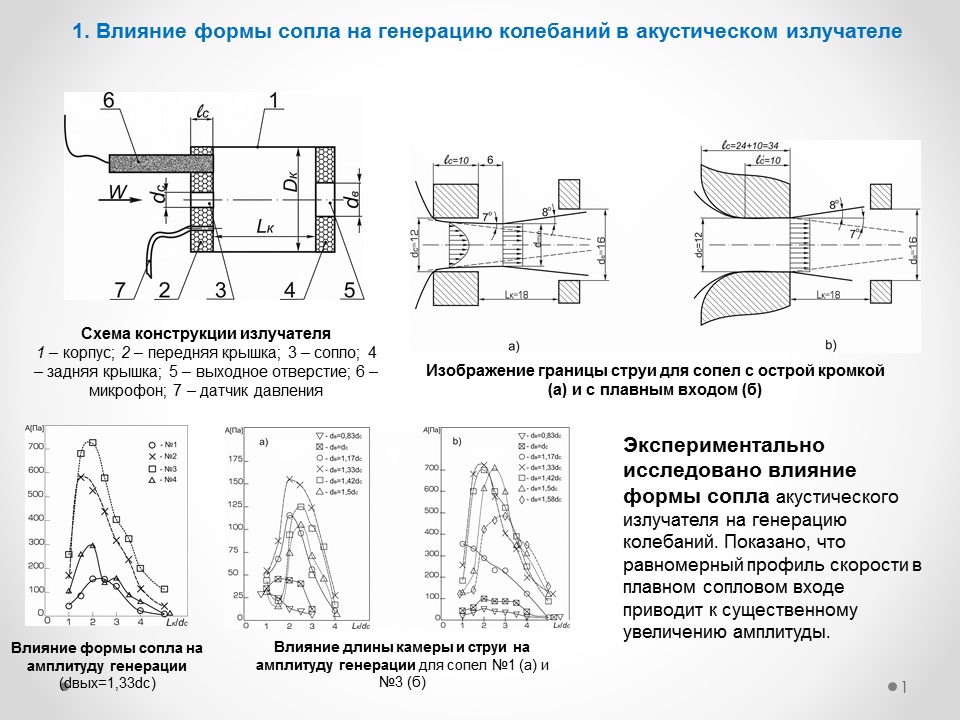
Выполнен комплекс исследований (аналитических, численных, экспериментальных и промысловых) процессов возбуждения упругих волн в потоках агентов, нагнетаемых в пласт. Выявлены закономерности и разработаны математические модели протекающих процессов.
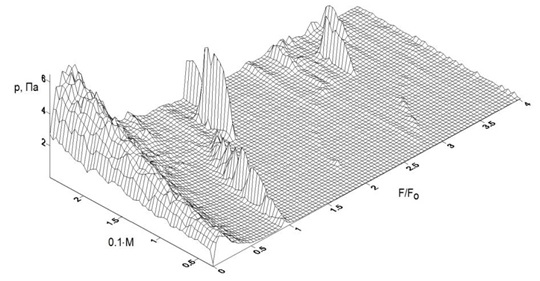
Рис.6. Частотная характеристика струйного излучателя
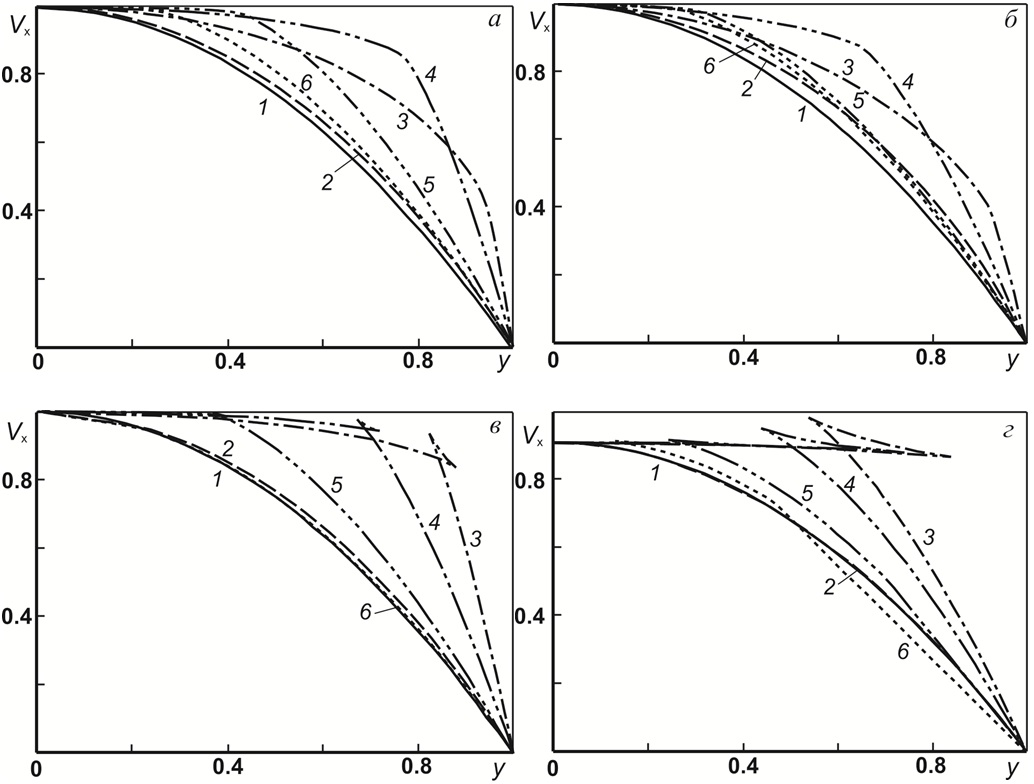
Рис. 1. Профили скорости для а – и ; б – и ; в – и ; г – и : 1 – ньютоновская жидкость; 2 – 6 –
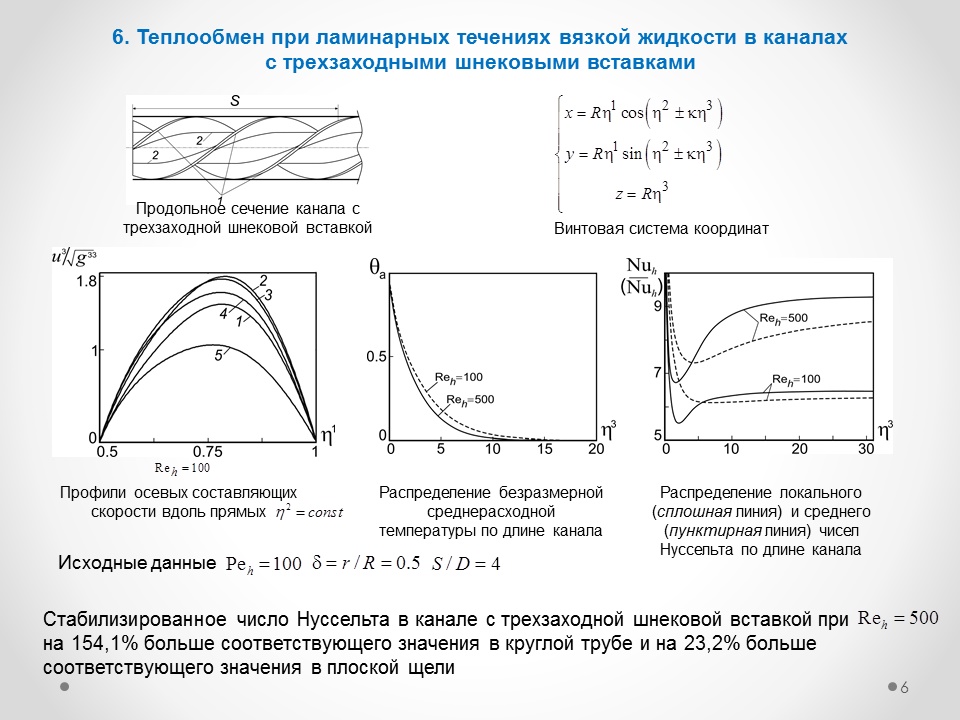
Доказана невозможность построения ортогональной винтовой системы координат. Получен наиболее простой и удобный вид винтовой системы координат. Проведен анализ всевозможных вариантов винтовых систем координат, применяемых для математического описания задач теплообмена и гидродинамики при течениях жидкостей в каналах, обладающих винтовой симметрией (инвариантность относительно сдвигов вдоль винтовых линий), которые широко используются в качестве интенсификаторов конвективного теплообмена (рис. 2).
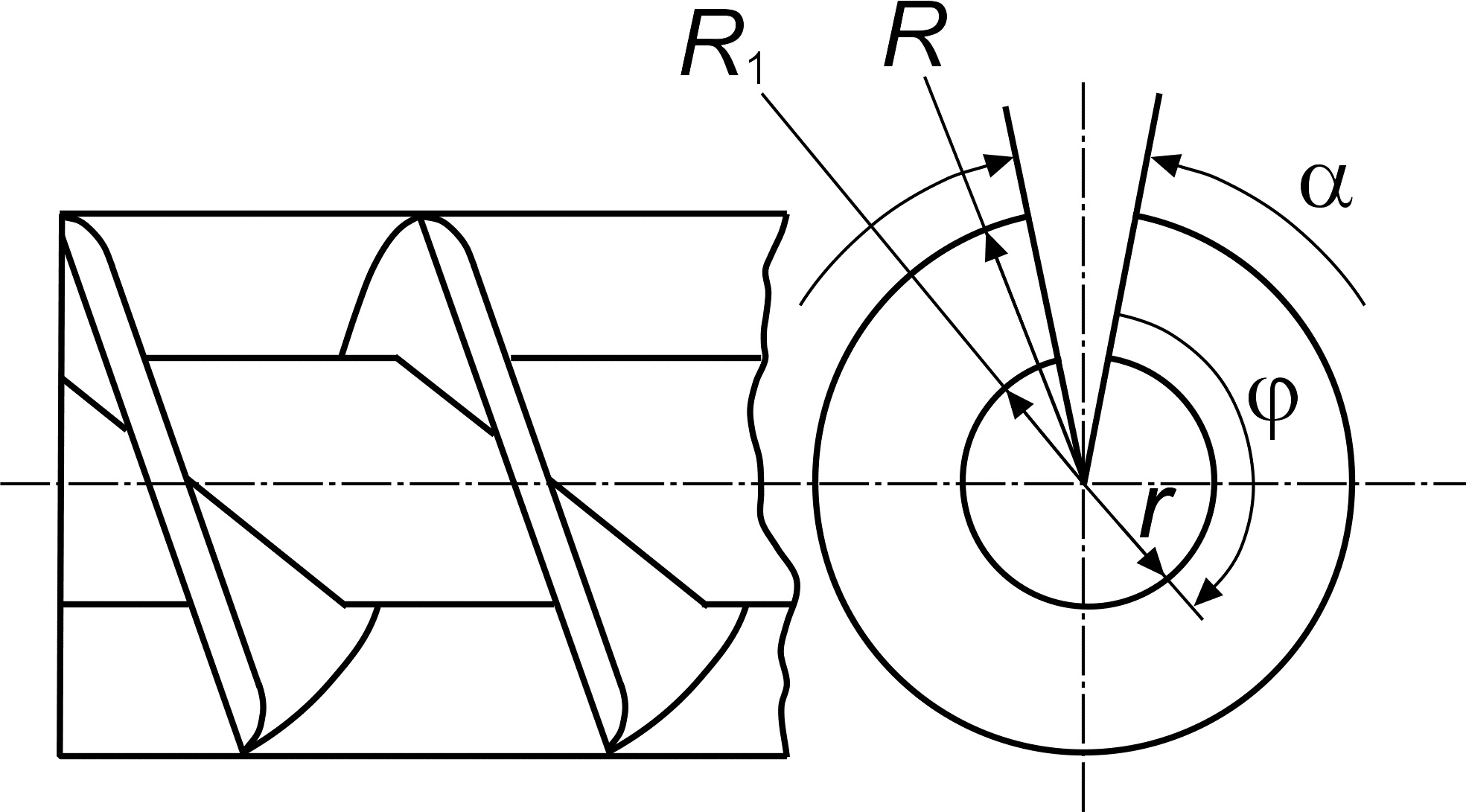
Рис. 2. Геометрия канала, обладающая винтовой симметрией
Экспериментально исследован переходный термический процесс в теле с однородной структурой (полиметилметакрилат (ПММА)) и измерена величина времени тепловой релаксации ПММА.
Исследуемый образец представляет склеенную из двух одинаковых листов ПММА пластину общей толщиной = 19,15 мм, шириной = 100 мм и длиной ≈ 112 мм. Теплофизические свойства ПММА [10, 11]: = 0,197 Вт/(м∙К); = 1188±0,5 кг/м3 (измерено нами); = 550 Дж/(кг∙К); = 3,015∙10-7 м2/с (рис. 1-15). Регистрация показаний термопар осуществлялась с помощью автоматизированной измерительной системы (АИС). Ввод-вывод аналоговых и цифровых сигналов осуществлялся с помощью устройства фирмы National Instruments PCI-6251, подключаемого к PCI-шине персонального компьютера (ПК).

Рис. 1. Установка для исследования переходных процессов при внезапном нагревании дискового образца из полиметилметакрилата (ПММА
Проведено три опыта: в первом и третьем образец внезапно опускался в кипящую воду, во втором опыте – быстро перемещался из кипящей воды в холодную воду. Переходные процессы, зарегистрированные в первом опыте, показаны на рис. 2
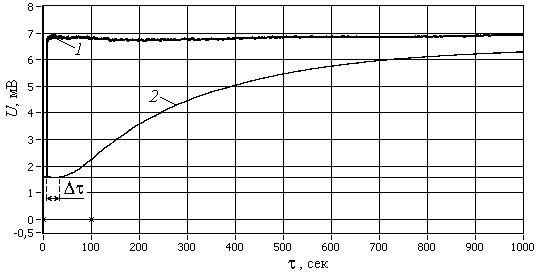
Рис. 2. Экспериментально зарегистрированные переходные процессы: 1 – показания термопары на наружной поверхности образца; 2 – то же в его центре
Незначительно изменяющиеся показания наружной термопары 1 после погружения образца в воду позволили принять её температуру в течение опыта неизменной. Средняя для трёх опытов задержка момента начала показаний внутренней термопары составила 27±1 с. Скорость распространения температурной волны до средней плоскости образца . Принимая , по формуле (, где ‑ скорость переноса, под которой одни исследователи понимают скорость переноса внутренней энергии (скорость звука), a – коэффициент температуропроводности) получено: 2,40±0,22 с.
Видимый на рис. 3-15 замедленный темп переходного процесса в опыте 2 по сравнению с опытами 1 и 3 объясняется менее интенсивной теплоотдачей поверхности образца в холодной воде по сравнению с кипящей водой
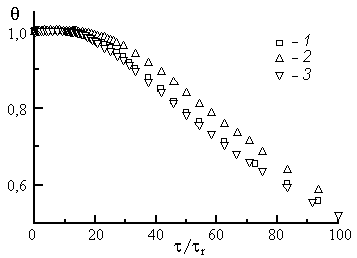
Рис. 3. Результаты измерений переходных процессов в трёх опытах
(1-3 – номера опытов)
Получено решение задачи о совместном течении в круглой трубе в средней части жидкости Гиезекуса и вязкой ньютоновской жидкости в пристеночной области трубы. Показано, что при определенных условиях значение градиента скорости сдвига в процессе течения двух рассматриваемых жидкостей меняется в меньших пределах по сравнению с течением единственной жидкости Гиезекуса, что способствует улучшению качественных характеристик полимерных изделий.
На рис. 4-15 представлены характерные профили скорости для различных значений и . Как следует из рисунка, чем меньше значение симплекса , тем более пологим становится профиль скорости в центральной части круглой трубы и тем меньше отклонение значения градиента скорости сдвига в этой области от нуля. При увеличении симплекса профили скорости все более вытянутыми становятся профили скорости в центральной части круглой трубы. Подробнее с результатами можно ознакомиться в работе пройдя по ссылке (http://elibrary.ru/item.asp?id=25672513)
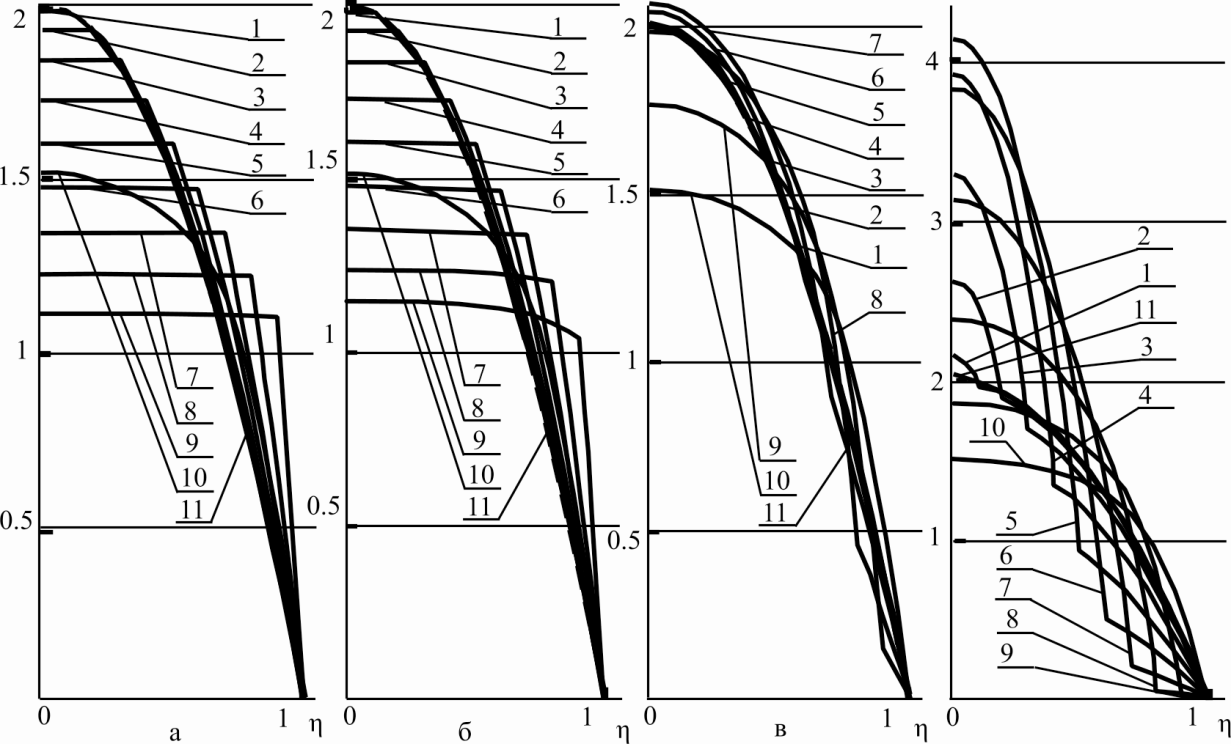
Рис. 4. Профили скорости при контактном течении жидкости «Giesekus» с параметрами: и вязкой ньютоновской жидкости при для различных значений : – линия 1; – линия 2; – линия 3; – линия 4; – линия 5; – линия 6; – линия 7; – линия 8; – линия 9; – линия 10; штриховая линия 11 – параболический закон для ньютоновской жидкости; а – ; б – ; в – ; г –
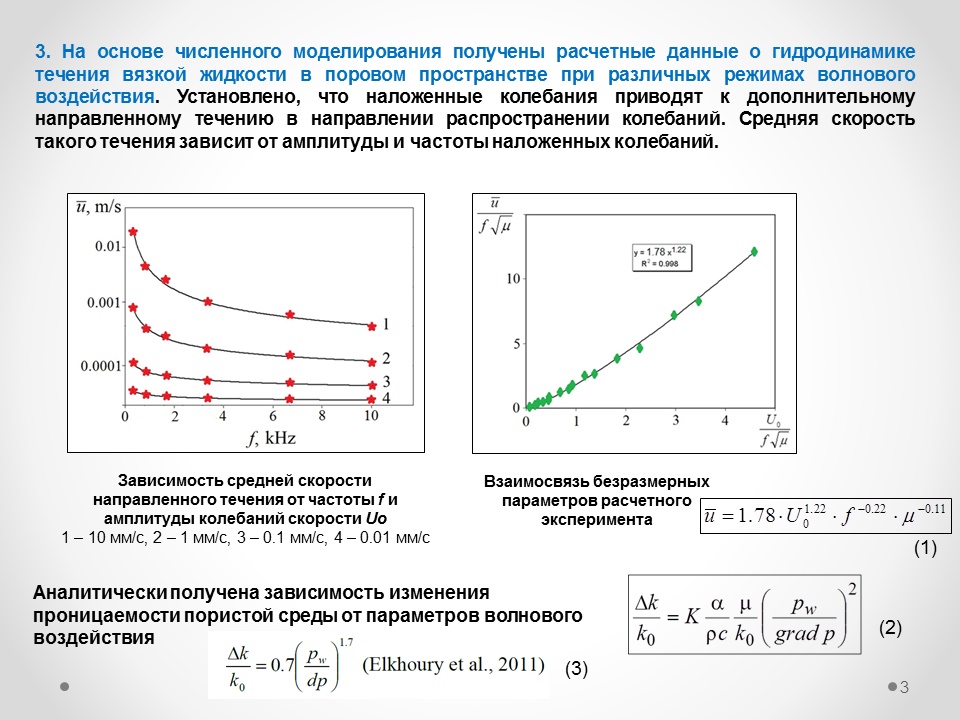
Разработан способ повышения эффективности добычи высоковязкой нефти за счет совмещения метода парогравитационного дренажа (SAGD) с волновым воздействием на пласт. На примере Ашальчинского месторождения показано существование оптимальных значений частоты волнового воздействия на пласт, позволяющее выбирать режим воздействия и технические средств его реализации
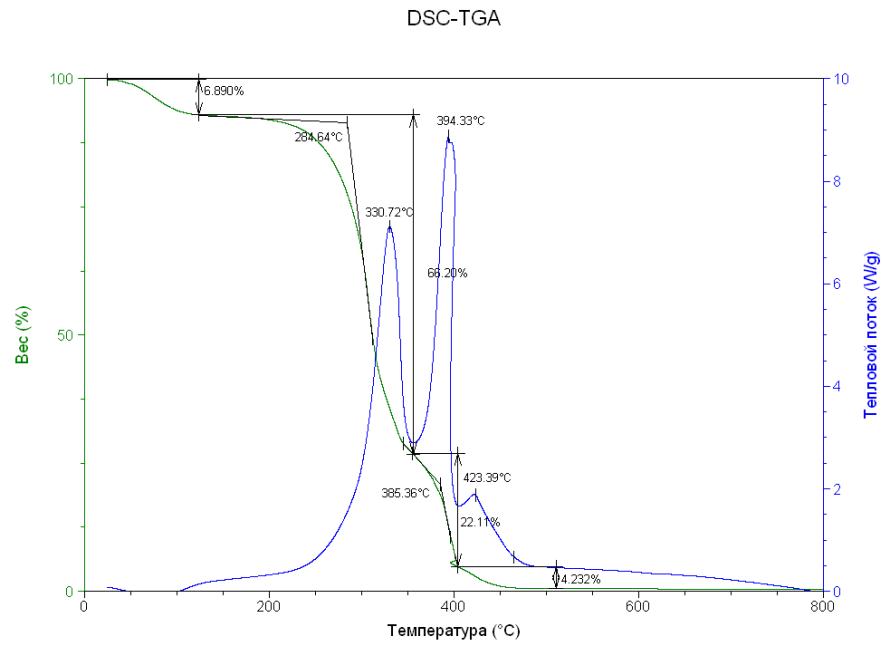
Рис.1. Схема тепловолнового воздействия на продуктивный пласт в условиях двухустьевых горизонтальных скважин; 1 – нагнетательная скважина, 2 – скважинные генераторы упругих волн, 3 – насосно-компрессорная труба, 4 – добывающая скважина, 5 – продуктивный пласт
Осуществлена проверка адекватности модели двухфазного запаздывания применительно к теплопроводности тел в быстропротекающих процессах при внезапном (однократном) и циклическом изменении граничных условий.
Созданы лабораторные установки для исследования переходных термических процессов при внезапном изменении граничных условий (рис. 2) и при циклическом (периодическом) изменении граничных условий. Для реализации циклических процессов создан стенд (рис. 3) с лабораторным регенератором переключающегося типа, содержащий рабочий участок (рис. 4), внутри которого размещена насадка из исследуемого материала (ПММА). Регистрация переходных термических процессов осуществляется с помощью автоматизированной измерительной системы (АИС), состоящей из ПК, платы National Instruments и пакета LabView. Регистрация сигналов, поступающих от ХК термопар диаметром 0,05/0,08 и 0,2 мм, при исследованиях ПММА осуществляется с частотой 50 гц.
На установке, показанной на рис. 2, получены первые данные о значениях и ПММА: с. Исследования предполагается продолжить на стенде, показанном на рис. 6-8.
Рис. 2. Установка для исследования переходных процессов при внезапном нагревании дискового образца из полиметилметакрилата (ПММА)
Рис. 3. Стенд с лабораторным регенератором переключающегося типа
Рис. 4. Рабочий участок лабораторного регенератора